Sample Continuous Time Frequency Spectrum Matlab

Generating a continuous signal and sampling it at a given rate is demonstrated here. In simulations, we may require to generate a continuous time signal and convert it to discrete domain by appropriate sampling.

For baseband signal, the sampling is straight forward. By Nyquist Shannon sampling theorem, for faithful reproduction of a continuous signal in discrete domain, one has to sample the signal at a rate higher than at-least twice the maximum frequency contained in the signal (actually, it is twice the one-sided bandwidth occupied by a real signal. For a baseband signal bandwidth ( to ) and maximum frequency in a given band are equivalent).

Matlab or any other simulation softwares  process everything in digital i.e, discrete in time. This is because, the signals are represented as discrete samples in computer memory. Therefore, we cannot generate a real continuous-time signal on it, rather we can generate a "continuous-like" signal by using a very very high sampling rate. When plotted, such signals look like a continuous signal.

Let's generate a simple continuous-like sinusoidal signal with frequency . In order to make it appear as a continuous signal when plotting, a sampling rate of is used.

          fs=500e3; %Very high sampling rate 500 kHz f=10e3; %Frequency of sinusoid nCyl=5; %generate five cycles of sinusoid t=0:1/fs:nCyl*1/f; %time index x=cos(2*pi*f*t);  plot(t,x) title('Continuous sinusoidal signal'); xlabel('Time(s)'); ylabel('Amplitude');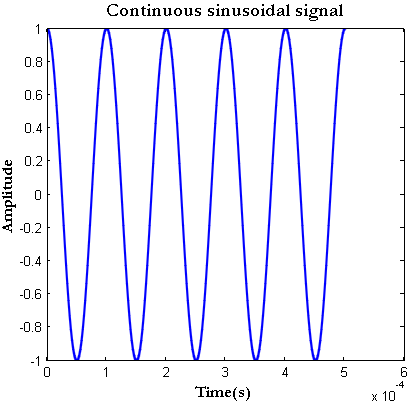        

Figure 1: Continuous time signal in Matlab

Pretending the above generated signal as a "continuous" signal, we would like to convert the signal to discrete-time equivalent by sampling. By Nyquist Shannon Theorem, the signal has to be sampled at at-least . Let's sample the signal at and then at for illustration.

          fs1=30e3; %30kHz sampling rate t1=0:1/fs1:nCyl*1/f; %time index x1=cos(2*pi*f*t1);  fs2=50e3; %50kHz sampling rate t2=0:1/fs2:nCyl*1/f; %time index x2=cos(2*pi*f*t2);  subplot(2,1,1); plot(t,x); hold on; stem(t1,x1); subplot(2,1,2); plot(t,x); hold on; stem(t2,x2);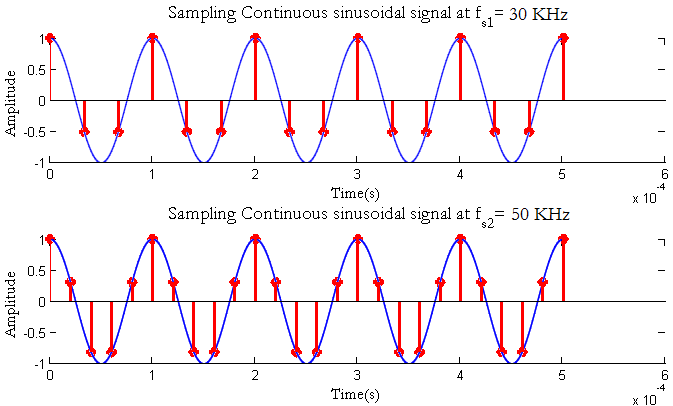        

Figure 2: Sampling a Continuous time signal in Matlab

Manipulating audio files in Matlab

Matlab's standard installation comes with a set of audio files. The audio files,that can be considered as one-dimensional vectors, can be inspected and played using xpsound command. With this command, we can visualize the audio files in three ways

● Time series (data-vector as function of time)
● Power spectral density (distribution of frequency content)
● Spectrogram (frequency content as function of time)

The output of the xpsound command plotting time-series plot of a sample audio file looks like this

Figure 3: Sound visualizer – xpsound

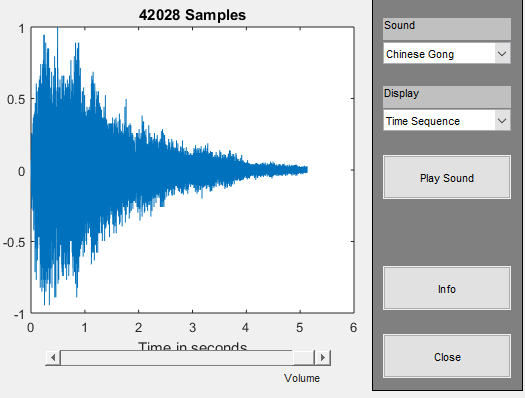
We can also load and plot the time-series plot using inbuilt Matlab commands as follows

          >> load('gong') %load the variables for the 'gong' audio file, this loads the sample frequency and the sample values >> Fs  %sampling frequency  Fs =          8192  >> y(1:10) %first 10 sample values in the file  ans =     -0.0027    -0.0045    -0.0074    -0.0110    -0.0128    -0.0173    -0.0223    -0.0223    -0.0200    -0.0092 >> t=0:1/Fs:length(y)/Fs-1/Fs; %time index >> figure;plot(t,y);xlabel('Time (s)'),ylabel('y')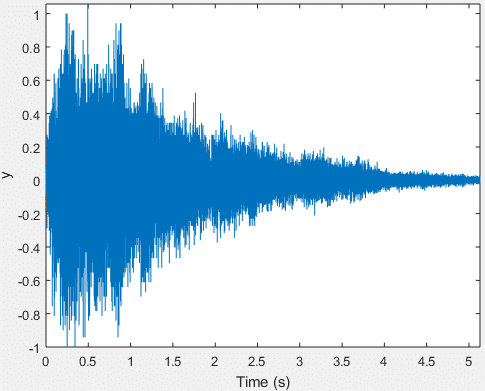        

Figure 4: 'Gong' sound visualized as time-series in Matlab

Example: DownSampling

In signal processing, downsampling is the process of throwing away samples without applying any low-pass filtering. Mathematically, downsampling by a factor of implies, starting from the very first sample we throw away every $M-1$ samples (i.e, keep every -th sample.

For example, if is a vector of input samples, downsampling by implies

Going back to the previous example of 'gong' audio vector loaded in the Matlab variable space, the downsampling operation can be coded as follows.

          >>M=2 % downsample by 2 >>y_down = y(1:M:end); % keep every M-th sample        

Note: Downsampling↗ is not same as decimation. Decimation↗ implies reducing the sampling rate of a signal by applying low-pass filtering as the first step and then followed by decimation.

Rate this article: (12 votes, average: 3.58 out of 5)

Reference

[1] Julius O smith III, "Spectral audio signal processing", Center for Computer Research in Music and Acoustics, Stanford.↗

Books by the author

porterhille1980.blogspot.com

Source: https://www.gaussianwaves.com/2014/07/sampling-a-signal-in-matlab/

Share this post